Memory access pattern matters

Posted by Filip Ekberg on 01 Jul 2013

Last week on BUILD there was a talk on Native Code Performance and Memory: The Elephant in the CPU, even though I didn't attend BUILD this year I watched it on Channel9 and I'd like to recap something from it that I find interesting. In many cases I think that we ignore the fact that we need to handle performance optimizations ourselves, we can't hide behind the CLR and the compiler all the time now, can we? Some say that Ignorance is Bliss, but in this case Ignorance might cause a lot of headache.

Let's start by taking an example from Eric Brumer's talk. Consider that we have the following three multi-dimensional arrays:

int N = 1000;
var A = new int[N, N];
var B = new int[N, N];
var C = new int[N, N];

Each matrix can be visualized like this, but in our case let's use random numbers later on. So as you can see it grows to the size of N in both X and Y axis.

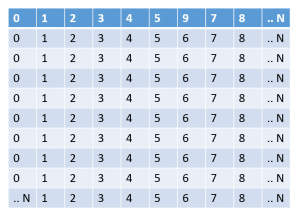
We can use the following code to fill these with random numbers:

var random = new Random();
for(int x = 0; x < N; x++)
{
    for(int y = 0; y < N; y++)
    {
        A[x, y] = random.Next();
        B[x, y] = random.Next();
        C[x, y] = random.Next();
    }
}

Let's now multiply A with B and store the result in C. This is where it all gets interesting. Let us first take a look at the code to perform this multiplication:

for (int i = 0; i < N; i++)
    for (int j = 0; j < N; j++)
        for (int k = 0; k < N; k++)
            C[i,j] += A[i,k] * B[k, j];

Running this on my machine takes about 12 seconds. We can do much better than that though! So what can we do in order to speed up the performance?

We can look at the memory access!

To some of you it might be obvious that when you access elements in memory that are closer to each other, this is faster than when accessing random memory over and over again. An array, or a row in a multi-dimensional array are stored in a sequence in memory. Here's an example of that:

Let's focus on B[k, j]. The k in this case tells us which row to load data from and the j which column. This means that when we are in the first iteration we will load the first value from the first column and the second time we will load the first value from the second row like this:

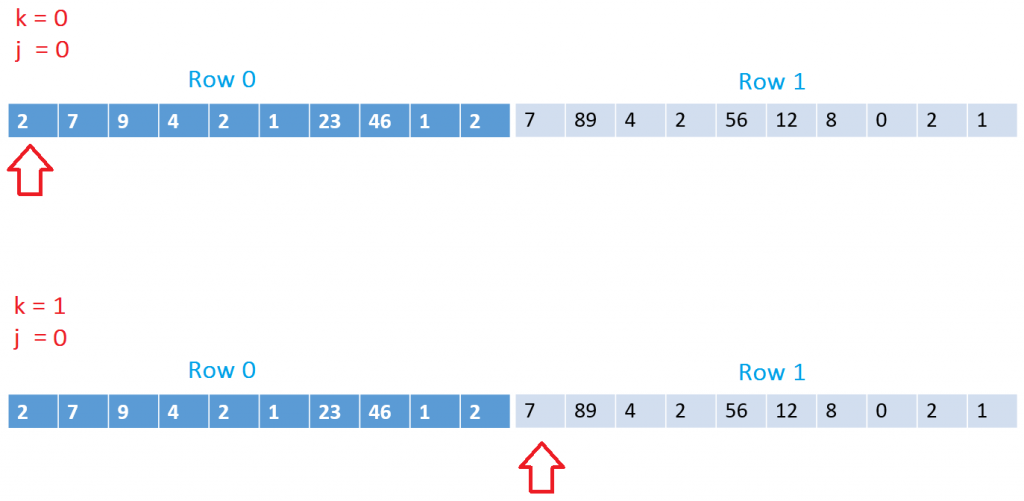
This is really bad because when we ask for the data in [0, 0] we will also have the surrounding data loaded into the cache. This means that the second time we iterate we will have to load a completely new chunk of data into the cache/memory because we don't have access to the row that we want.

So how do we fix this?

It's quite simple and probably obvious. We can just swap the two inner loops so that we instead process each column in each row before we change row:

for (int i = 0; i < N; i++)
    for (int k = 0; k < N; k++)
        for (int j = 0; j < N; j++)
            C[i, j] += A[i, k] * B[k, j];

This actually resulted in 60% faster execution on my machine and in low level programming (C/C++) I imagine the impact would be much larger. The reason that I wanted to bring all this up is because it's important that we don't forget about these things, even if we live in a managed world. I also strongly advice to go over to Channel9 and watch that presentation by Eric Brumer.

The samples in this post are the same that Eric brings up in his presentation among a lot of other great examples of how we should work with our code memory efficiently. Read more about Optimize Data Structures and Memory Access Patterns to Improve Data Locality.

Is this obvious? Do you consider these things in your day-to-day work? Leave your thoughts in the comment field below!

Here's a complete code sample that I used to measure the times:

int N = 1000;
var A = new int[N,N];
var B = new int[N, N];
var C = new int[N, N];
var random = new Random();
for(int x = 0; x < N; x++)
{
    for(int y = 0; y < N; y++)
    {
        A[x, y] = random.Next();
        B[x, y] = random.Next();
        C[x, y] = random.Next();
    }
}

var watch = new Stopwatch();
watch.Start();

for (int i = 0; i < N; i++)
    for (int j = 0; j < N; j++)
        for (int k = 0; k < N; k++)
            C[i,j] += A[i,k] * B[k, j];

watch.Stop();

Console.WriteLine("Time: {0}ms", watch.ElapsedMilliseconds);


watch.Reset();
watch.Start();

// 60% Faster than the loop above!
for (int i = 0; i < N; i++)
    for (int k = 0; k < N; k++)
        for (int j = 0; j < N; j++)
            C[i, j] += A[i, k] * B[k, j];

watch.Stop();

Console.WriteLine("Time: {0}ms", watch.ElapsedMilliseconds);

Follow @fekberg